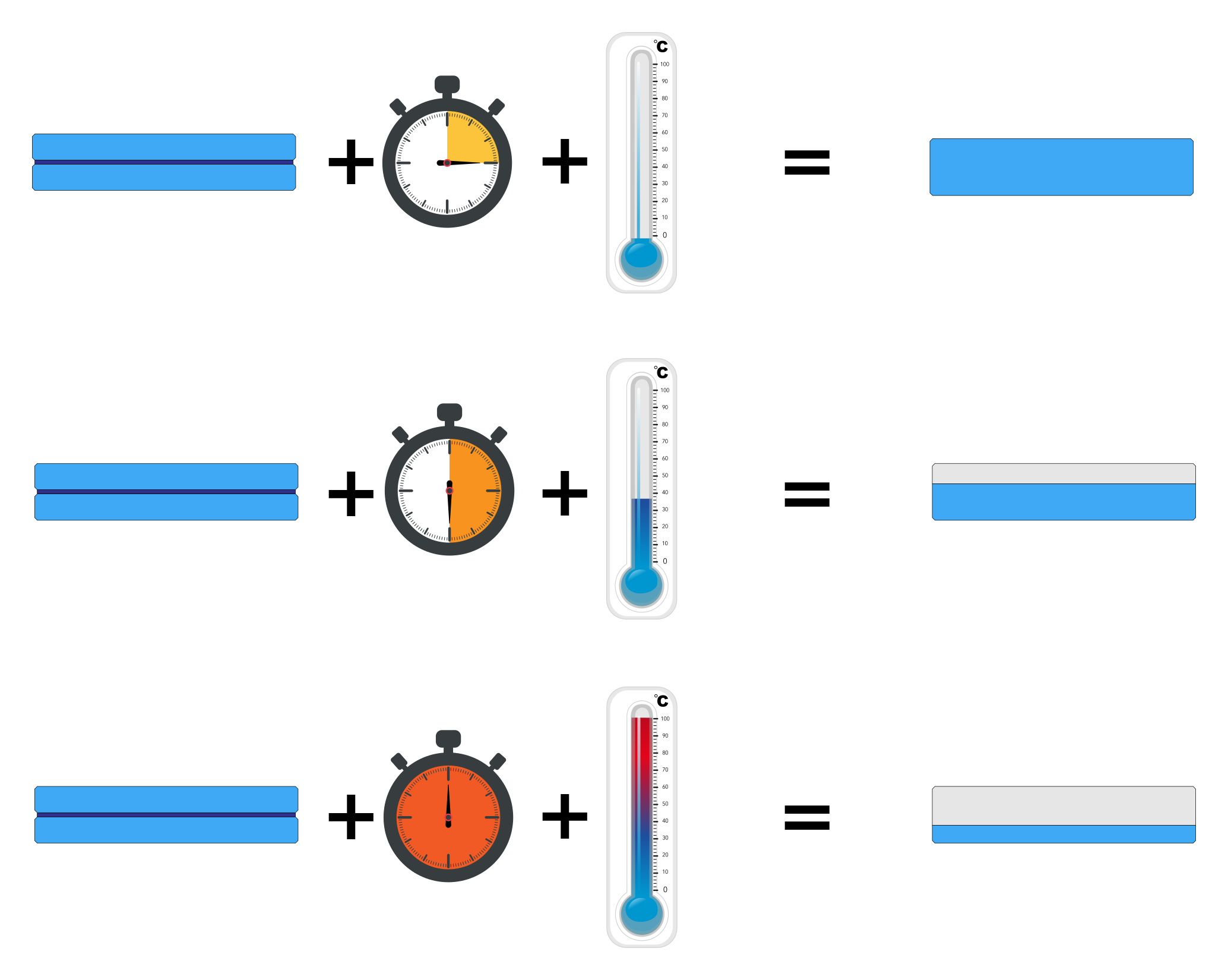
I vetri stratificati sono costituiti dall’unione per pressaggio e riscaldamento di due o più lastre di vetro con uno strato di materiale elastomerico interposto, aderente su tutta la superficie della lastra.
Per tali tipologie di vetri, è possibile valutare gli effetti indotti dai carichi agenti simulando tali azioni agenti su una piastra di spessore “equivalente”. Si adotta quindi un metodo di “Livello 1” (secondo CNR-DT 210/2013), con il quale l’elemento di vetro stratificato può essere modellato come un elemento di vetro monolitico che presenta lo stesso comportamento a flessione.
Le caratteristiche meccaniche dell’elastomero sono fortemente dipendenti dal tempo e dalla temperatura. Il comportamento di un elemento di vetro stratificato è intermedio fra quello di un elemento a strati indipendenti e quello di un elemento monolitico, a seconda del grado di accoppiamento a taglio offerto dall’intercalare.
Al variare del polimero, dei carichi, della geometria, della composizione del vetro stratificato, il coefficiente di trasferimento del taglio assume un valore compreso tra 1, perfetto trasferimento del taglio e comportamento complessivo dello stratificato assimilabile a quello di un vetro monolitico avente spessore equivalente (monolithic limit), e 0, incapacità del polimero di trasferire azioni di taglio (layered limit).
- dimensioni dei lati;
- spessori delle lastre;
- spessore e tipologia dell'intercalare (modulo di taglio G);
- condizione di vincolo e di carico.
Il momento di inerzia equivalente che consente di definire gli spessori efficaci, in relazione alla deformabilità a taglio dell’intercalare, alla geometria e alle condizioni di vincolo della struttura, è calcolato secondo il modello Enhanced Effective Thikness (EET). Tale modello, proposto in [Galuppi, Royer-Carfagni, 2012a], [Galuppi, Royer-Carfagni, 2012b], [Galuppi et al., 2013a], è un modello semplice, adatto al calcolo di spessori equivalenti sia per geometrie di tipo “trave” che di tipo “piastra”.
Possono quindi essere definiti i seguenti valori:
- spessore efficace per il calcolo della deflessione: spessore della trave monolitica che presenta la stessa deflessione massima della trave di vetro stratificato in esame;
- spessore efficace per il calcolo delle tensioni: spessore della trave monolitica che presenta la stessa tensione massima di ciascuno degli strati della lastra di vetro stratificato in esame.
Le distanze dei baricentri dei singoli strati dal baricentro dell’intera lastra sono pari a:
- distanza d1 = 5.5 mm;
- distanza d2 = 5.5 mm.
La condizione di carico e di vincolo è del tipo:
Pertanto, il coefficiente dimensionale Ψ, che dipende dalla condizione di carico e vincolo del caso in esame, è pari a 2.8E-6.
Le caratteristiche meccaniche del vetro risultano:
- modulo di Young del vetro E = 70000;
- coefficiente di Poisson del vetro v = 0.22.
Le caratteristiche meccaniche dell’intercalare dipendono dalla temperatura e dalla durata del carico. Per il caso in esame, si adotta un modulo di taglio dell’intercalare pari a 0.56 Mpa.
In definitiva, per la lastra di vetro stratificato in esame, gli spessori efficaci calcolati con il servizio EET risultano pari a:
- spessore efficace per il calcolo della deflessione: 18,67 mm;
- spessore efficace per il calcolo delle tensioni della lastra 1: 19,84 mm;
- spessore efficace per il calcolo delle tensioni della lastra 2: 19,84 mm.
Infine, tali spessori possono essere utilizzati nel modello agli elementi finiti per il calcolo delle tensioni (th = 19,84 mm) e delle deformazioni (th = 18,67 mm).
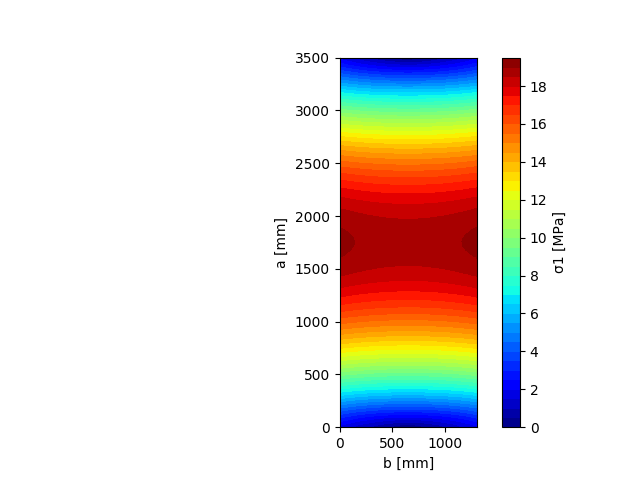
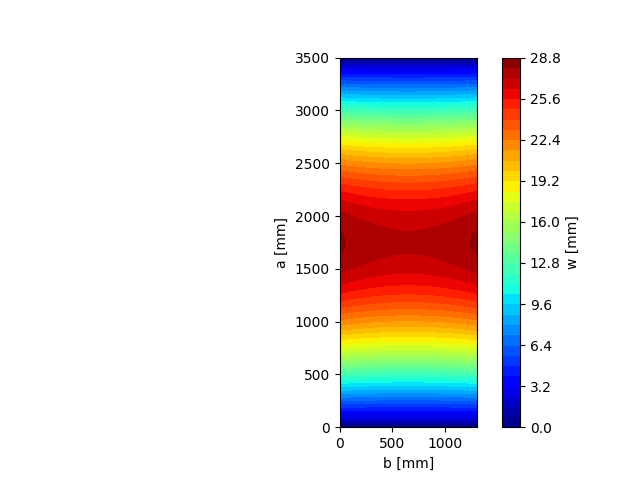
In aggiunta, il servizio CHK calcola gli spessori equivalenti di lastre stratificate a 2 strati, esegue la modellazione agli elementi finiti e verifica automaticamente che la stratigrafia scelta soddisfi le verifiche di resistenza e di deformazione.



